Generalized linear models

Chapter 12

Introduction

Habitat fragmentation alters the movement and composition of wildlife communities, with cascading effects on the distribution of parasites and the pathogens they carry. In the western United States, the black-legged tick Ixodes pacificus transmits several bacteria, including Borrelia burgdorferi, which causes Lyme disease. These ticks feed on a variety of hosts, including rodents, deer, and predators, and their infection rates are shaped by the diversity and abundance of those host species.

Some pathogens, like B. burgdorferi, rely entirely on horizontal transmission-ticks must feed on an infected host to acquire and later transmit the bacteria. Others, like Borrelia miyamotoi, can be transmitted vertically from tick to offspring. Understanding how these ecological and evolutionary differences interact with landscape features and wildlife communities is key to predicting disease risk.

In this lab, we will test whether the diversity of rodent hosts can help explain the density of B. burgdorferi-infected ticks across forest fragments in Northern California. This is the same question investigated by the Swei Lab at San Francisco State University, which investigates how landscape isolation and wildlife community metrics predict tick-borne pathogen distribution.

Figure 1. (A) Tick transmission cycle. Barbour & Zückert, Nature 390:553–554 (1997). (B) Adult female western blacklegged tick, Ixodes pacificus. CDC/Loftis et al.

Upon completion of this lab, you should be able to:

1. Fit GLMs using R.
2. Interpret GLM outputs, including coefficients and AIC values.
3. Compare GLMs to models introduced in previous labs.
4. Fit GLMMs with random effects using glmmTMB().

References:

• Shaw et al. 2024

Worked example

Suppose you are studying how the number of bird visits to a feeder changes with outdoor temperature. You observe a series of 10-minute intervals and count how many birds visit a feeder at different temperatures throughout the day. The response variable is a count ; discrete, non-negative, and often right-skewed. Because of this, a linear model (which assumes normally distributed residuals and constant variance) would not be appropriate. Instead, we use a generalized linear model (GLM) with a Poisson distribution, which is designed for modeling count data.

GLMs can be written in the form:

g(μ) = β₀ + β₁X

where g() is the link function. For Poisson models, this is the log function. This equation says that the log of the expected count (bird visits) is a linear function of the predictor (temperature).

# Fit a Poisson GLM
glm(bird_visits ~ temperature, family = "poisson", data = birds)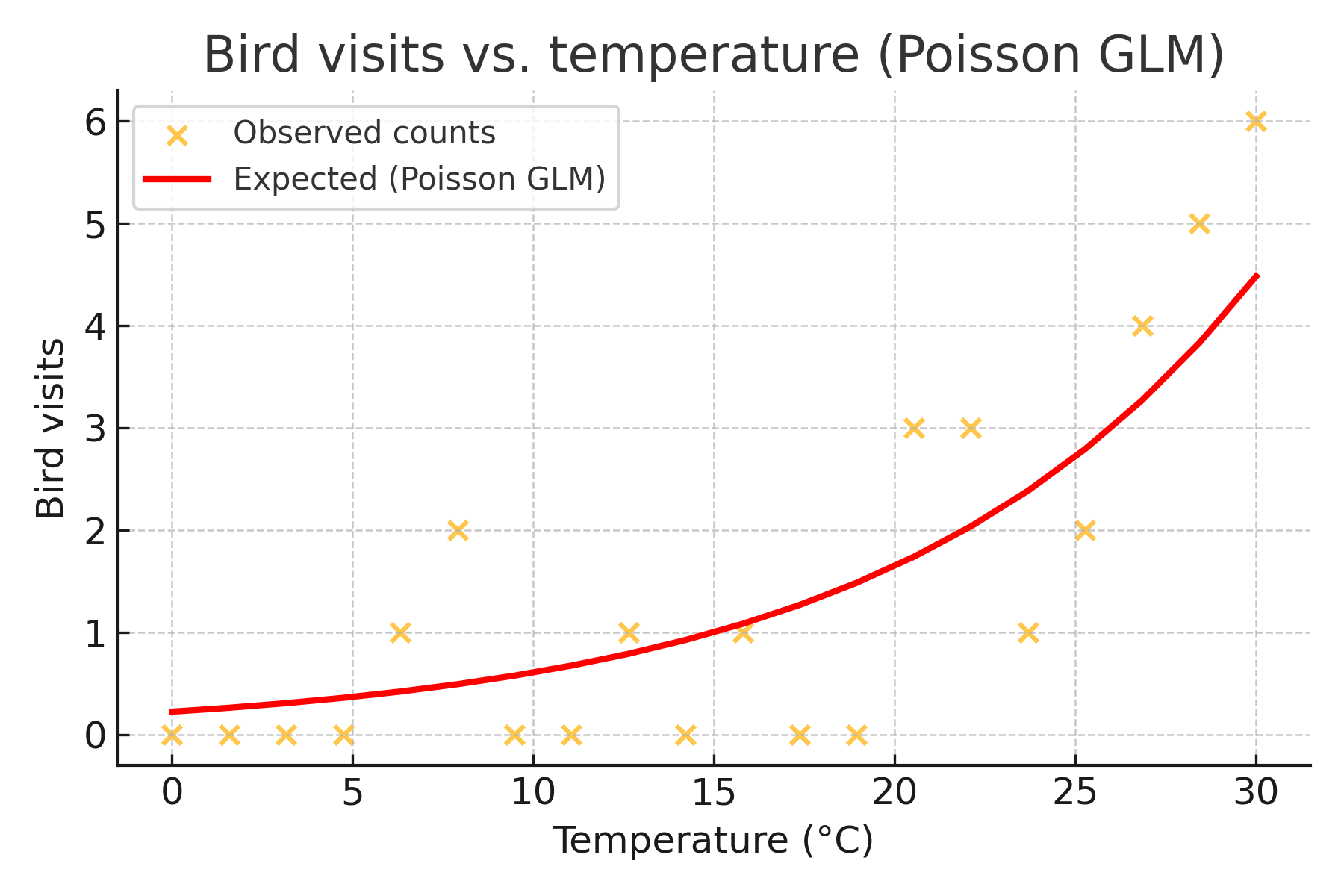

Figure 3. Hypothetical Poisson GLM showing bird visits as a function of temperature. The red line is the expected count under a Poisson model.

This plot helps illustrate two things. First, count data are right-skewed and discrete. Second, the relationship between temperature and bird visits is curved on the original scale, but linear when viewed on the log scale; exactly what the Poisson GLM models.

To decide which predictors to include, we can compare models using the Akaike Information Criterion (AIC). AIC rewards models that fit the data well but penalizes complexity. The model with the lowest AIC is considered the best among those being compared.

What if the bird visits were measured at multiple times of day in the same location, and we suspected the counts might be correlated by location? In that case, we could use a generalized linear mixed model (GLMM), which allows us to include random effects such as Site or observer. GLMMs are extensions of GLMs that account for grouping or repeated measures in the data.

Stop, Think: Interpret the model output from R (GLM table). Stop and review the Worked example. Think about how you can obtain each value in the model output.

GLMs are most often used when you want to model a response variable that is not continuous and normally distributed. But how do we know if one GLM is better than another? One common method is to use the Akaike Information Criterion (AIC), which balances model fit and complexity. A model with a lower AIC is considered better; it explains more of the variation in the data with fewer or more efficient predictors.

Finally, what if we suspect that observations are grouped, and that there's unmeasured variation across those groups? This is where generalized linear mixed models (GLMMs) come in. GLMMs allow us to include random effects, such as variation by site or subject, which helps us avoid biased estimates. These models are especially useful for repeated measures or nested data; like multiple tick samples taken from the same location.

# Fit a Poisson GLMM
library(glmmTMB)
glmm(bird_visits ~ temperature + (1 | location), 
     family = poisson, data = birds)

Materials and Methods

• R and RStudio
• package ggplot2
• package glmmTMB
• tick.csv

Variable descriptions: In this lab, we focus on three variables from the dataset. DIN_Bbsl refers to the density of infected nymphs (ticks) carrying Borrelia burgdorferi sensu lato. Rodent_Rich is the number of different rodent species observed at a site. Predator_Shannon_wCat is the Shannon diversity index of predator species (including cats), and Site identifies each sampled location.

Today’s activity on rodent diversity and infected tick density is organized into one main exercise that explores how rodent communities influence tick-borne pathogen dynamics. This exercise will help us apply GLMs to real ecological data, interpret R model outputs, and check model assumptions.

Before we begin fitting models, let’s load the dataset. It contains site-level summaries of tick density, rodent richness, predator diversity, and other ecological variables collected from forest fragments across Northern California. These data were collected repeatedly at each site across multiple years. We'll fit models that account for variation across both sites and years using random effects.

1. Import the data Let’s import the "tick.csv" dataset and explore it.

2. Fit a Poisson GLM

We are using a Poisson model here because our response variable(tick infection density)is a count. Poisson models are designed for count data that are non-negative integers and often right-skewed. In Poisson GLMs, the variance increases with the mean, which often fits ecological count data better than assuming constant variance and normality.

# Fit GLM with Poisson family
tick_glm <- glm(DIN_Bbsl ~ Rodent_Rich, family = "poisson", data = tick)
summary(tick_glm)

# GLM output
summary(tick_glm)

3. Plot your GLM predictions

After fitting a GLM, it’s useful to visualize the model predictions alongside your raw data. To do this, we can use the predict() function, which takes a fitted model and returns predicted values. These predictions can then be added as a new column in our dataset and plotted against the observed data to assess model fit and shape.

# Add model predictions to the dataset
tick$predicted <- predict(tick_glm, type = "response")

# Plot observed and predicted values
ggplot(tick, aes(x = Rodent_Rich, y = DIN_Bbsl)) +
  geom_point(alpha = 0.6) +
  geom_line(aes(y = predicted), color = "red", size = 1) +
  labs(
    x = "Rodent richness",
    y = "Density of infected nymphs (DIN_Bbsl)",
    title = "Predicted vs. Observed: GLM for Infected Tick Density") +
  theme_minimal()

4. Plot model diagnostics

After fitting a model, it’s important to assess how well it fits the data. In this step, we’ll visualize the residuals and fitted values to check for overdispersion and other patterns that might indicate poor model fit.

# Diagnostic plots for GLM
plot(tick_glm)

5. Add another predictor

In Chapter 10, we explored how using two explanatory variables together can help reveal interactions or explain more variation in a response. Here, we’ll test whether adding another biologically relevant predictor (predator diversity) improves our model of tick infection density. This step mirrors the idea of exploring multiple factors at once, just as we did with two-way ANOVA.

# Compare two GLMs with AIC
tick_glm2 <- glm(DIN_Bbsl ~ Rodent_Rich + Predator_Shannon_wCat, family = \"poisson\", data = tick)
AIC(tick_glm, tick_glm2)

Great Work!